Case Study 1: Distance vs. Displacement
Amit walks 3 km east and then 4 km north. His total distance is 7 km, but his displacement is the straight-line distance from the starting point to the final point.
Questions:
- Total distance covered = ?
(a) 3 km (b) 4 km (c) 5 km (d) 7 km
Answer: (d) - Displacement = ?
(a) 3 km (b) 4 km (c) 5 km (d) 7 km
Answer: (c) - Displacement can be:
(a) greater than distance (b) smaller than distance (c) equal to or smaller than distance (d) none
Answer: (c) - Which theorem is used to calculate displacement?
(a) Pythagoras theorem (b) Bernoulli’s theorem (c) Work-energy theorem (d) None
Answer: (a) - Distance is a:
(a) scalar (b) vector (c) tensor (d) none
Answer: (a)
Case Study 2: Average Speed and Average Velocity
Ravi goes from home to school (10 km) in 30 minutes and returns by the same route in another 30 minutes.
Questions:
- Total distance travelled = ?
(a) 10 km (b) 20 km (c) 30 km (d) 40 km
Answer: (b) - Total displacement = ?
(a) 0 (b) 10 km (c) 20 km (d) 40 km
Answer: (a) - Average speed = ?
(a) 20 km/h (b) 30 km/h (c) 40 km/h (d) 0 km/h
Answer: (a) - Average velocity = ?
(a) 0 (b) 20 km/h (c) 30 km/h (d) 40 km/h
Answer: (a) - Difference arises because:
(a) speed is scalar, velocity is vector
(b) both are vector
(c) both are scalar
(d) none
Answer: (a)
Case Study 3: Velocity-Time Graph (Uniform Motion)
A car moves with constant velocity of 20 m/s for 10 s. Its velocity-time graph is a straight line parallel to the time axis.
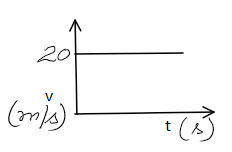
Questions:
- Slope of velocity-time graph = ?
(a) velocity (b) acceleration (c) displacement (d) none
Answer: (b) - Acceleration in this case = ?
(a) 0 (b) 20 m/s² (c) 10 m/s² (d) 5 m/s²
Answer: (a) - Distance travelled = area under the graph = ?
(a) 100 m (b) 200 m (c) 300 m (d) 400 m
Answer: (d) - The motion is:
(a) uniform (b) accelerated (c) retarded (d) non-uniform
Answer: (a) - Graph of uniform motion is:
(a) straight line sloping upwards (b) parallel to time axis (c) parallel to velocity axis (d) none
Answer: (b)
Case Study 4: Acceleration
A bike increases its velocity from 10 m/s to 30 m/s in 5 s.
Questions:
- Initial velocity (u) = ?
(a) 0 (b) 10 m/s (c) 30 m/s (d) 5 m/s
Answer: (b) - Final velocity (v) = ?
(a) 10 m/s (b) 30 m/s (c) 40 m/s (d) 20 m/s
Answer: (b) - Acceleration = (v – u)/t = ?
(a) 2 m/s² (b) 4 m/s² (c) 5 m/s² (d) 6 m/s²
Answer: (a) - Equation used:
(a) v = u + at (b) s = ut + ½at² (c) v² – u² = 2as (d) all of these
Answer: (a) - Type of acceleration = ?
(a) uniform (b) non-uniform (c) zero (d) none
Answer: (a)
Case Study 5: Equation of Motion (s = ut + ½at²)
A bus starts from rest and moves with acceleration 2 m/s². Find the distance travelled in 5 s.
Questions:
- u = ?
(a) 0 (b) 2 m/s (c) 5 m/s (d) 10 m/s
Answer: (a) - a = ?
(a) 2 m/s² (b) 5 m/s² (c) 10 m/s² (d) 0
Answer: (a) - t = ?
(a) 2 s (b) 5 s (c) 10 s (d) 0
Answer: (b) - s = ut + ½at² = ?
(a) 10 m (b) 15 m (c) 20 m (d) 25 m
Answer: (d) - Final velocity after 5 s = u + at = ?
(a) 5 m/s (b) 8 m/s (c) 10 m/s (d) 10 m/s
Answer: (c)
Case Study 6: Free Fall
A stone is dropped from a height of 20 m. It falls freely under gravity.
Questions:
- Initial velocity (u) = ?
(a) 0 (b) 9.8 m/s (c) 20 m/s (d) none
Answer: (a) - Acceleration = ?
(a) 0 (b) 9.8 m/s² (c) 20 m/s² (d) 5 m/s²
Answer: (b) - Equation used = ?
(a) v = u + at (b) s = ut + ½at² (c) v² – u² = 2as (d) all
Answer: (d) - Time taken to fall (approx) = ?
(a) 1 s (b) 2 s (c) 3 s (d) 4 s
Answer: (b) - Type of motion = ?
(a) uniform (b) uniformly accelerated (c) non-uniform (d) none
Answer: (b)
Case Study 7: Uniform Circular Motion
A car moves around a circular track of radius 7 m at constant speed 14 m/s.

Questions:
- Distance in 1 revolution = ?
(a) 14 m (b) 22 m (c) 44 m (d) 2πr
Answer: (d) - Speed remains:
(a) constant (b) changing (c) zero (d) none
Answer: (a) - Velocity remains:
(a) constant (b) changing due to direction (c) zero (d) none
Answer: (b) - Acceleration is directed towards:
(a) tangent (b) centre (c) outward (d) none
Answer: (b) - This acceleration is called:
(a) tangential (b) centrifugal (c) centripetal (d) none
Answer: (c)
Case Study 8: Non-uniform Motion
A bus moves 2 km in the first 5 min, 3 km in next 5 min, and 5 km in next 5 min.
Questions:
- Time total = ?
(a) 10 min (b) 15 min (c) 20 min (d) 30 min
Answer: (b) - Distance total = ?
(a) 5 km (b) 8 km (c) 10 km (d) 12 km
Answer: (c) - Motion is:
(a) uniform (b) non-uniform (c) accelerated (d) none
Answer: (b) - Average speed = ?
(a) 30 km/h (b) 40 km/h (c) 20 km/h (d) 10 km/h
Answer: (a) - Average velocity = ?
(a) same as average speed if straight path (b) zero (c) infinite (d) none
Answer: (a)
Case Study 9: Retardation
A car moving at 20 m/s comes to rest in 5 s after brakes are applied.
Questions:
- Initial velocity = ?
(a) 0 (b) 5 m/s (c) 20 m/s (d) 10 m/s
Answer: (c) - Final velocity = ?
(a) 0 (b) 5 m/s (c) 10 m/s (d) 20 m/s
Answer: (a) - Acceleration = (v – u)/t = ?
(a) –4 m/s² (b) 4 m/s² (c) –2 m/s² (d) 2 m/s²
Answer: (a) - Negative acceleration is called:
(a) retardation (b) deceleration (c) both (d) none
Answer: (c) - Distance covered in this time = ?
(a) 25 m (b) 50 m (c) 100 m (d) 200 m
Answer: (b)
Case Study 10: Motion Graph Interpretation
A velocity-time graph shows a car moving with uniform acceleration from 0 to 20 m/s in 10 s.
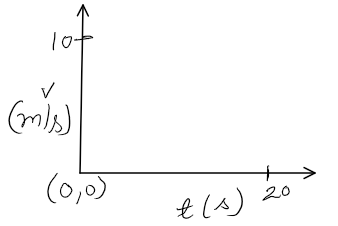
Questions:
- Type of graph:
(a) distance-time (b) velocity-time (c) acceleration-time (d) none
Answer: (b) - Slope of this graph = ?
(a) velocity (b) acceleration (c) displacement (d) none
Answer: (b) - Acceleration = slope = (20 – 0)/(10 – 0) = ?
(a) 1 m/s² (b) 2 m/s² (c) 3 m/s² (d) 4 m/s²
Answer: (a) - Distance travelled = area under graph = ?
(a) 50 m (b) 100 m (c) 150 m (d) 200 m
Answer: (b) - Nature of motion = ?
(a) uniform (b) accelerated (c) retarded (d) none
Answer: (b)
