Case Study 1: Road Crossing (Vertically Opposite Angles)
Two roads intersect each other at a point and form angles. At the intersection, ∠AOC = 70°.
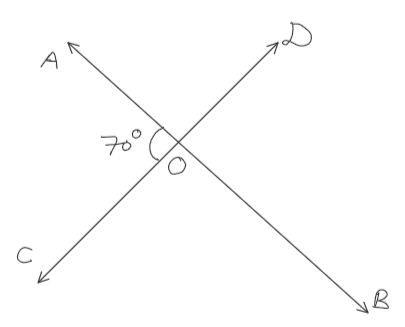
Questions:
- Vertically opposite angle of ∠AOC is:
(a) ∠AOB (b) ∠BOD (c) ∠COD (d) none
Answer: (c) - Value of ∠COD is:
(a) 70° (b) 110° (c) 90° (d) 100°
Answer: (a) - ∠AOC + ∠BOC form:
(a) linear pair (b) vertically opposite (c) supplementary (d) both (a) and (c)
Answer: (d) - Sum of ∠AOC + ∠COD =
(a) 70° (b) 140° (c) 180° (d) 90°
Answer: (c) - Which property is applied?
(a) Vertically opposite angles are equal (b) Angles in triangle (c) Parallel line rule (d) none
Answer: (a)
Case Study 2: Railway Tracks (Parallel Lines)
A railway line is crossed by a transversal bridge. The corresponding angles formed are ∠1 = 65°.
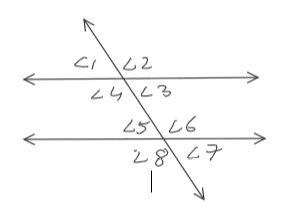
Questions:
- If lines are parallel, ∠5 = ?
(a) 115° (b) 65° (c) 45° (d) 75°
Answer: (b) - Alternate interior angles are:
(a) equal (b) supplementary (c) complementary (d) none
Answer: (a) - ∠1 + ∠2 on same side of transversal =
(a) 90° (b) 120° (c) 180° (d) 270°
Answer: (c) - Which theorem is used?
(a) Parallel line theorem (b) Pythagoras (c) Triangle sum (d) none
Answer: (a) - If ∠1=65°, ∠3=?
(a) 65° (b) 115° (c) 75° (d) none
Answer: (b)
Case Study 3: Linear Pair
Two adjacent angles form a straight line. If ∠PQR = 120°, find ∠RQS.
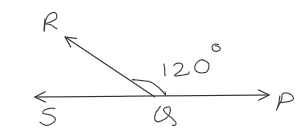
Questions:
- ∠PQR + ∠RQS =
(a) 90° (b) 120° (c) 180° (d) 270°
Answer: (c) - If ∠PQR=120°, ∠RQS=?
(a) 50° (b) 60° (c) 70° (d) 80°
Answer: (b) - Linear pair are always:
(a) complementary (b) supplementary (c) equal (d) none
Answer: (b) - Linear pair theorem states:
(a) sum = 180° (b) sum = 90° (c) equal angles (d) none
Answer: (a) - ∠PQR and ∠RQS are:
(a) vertically opposite (b) linear pair (c) alternate interior (d) none
Answer: (b)
Case Study 4: Triangle Angles
In a triangle, ∠A = 50°, ∠B = 60°.
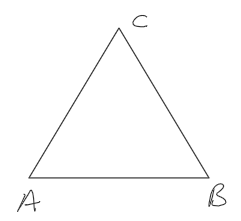
Questions:
- ∠C=?
(a) 60° (b) 70° (c) 80° (d) 90°
Answer: (b) - Theorem used:
(a) Triangle angle sum = 180° (b) Pythagoras (c) Exterior angle theorem (d) none
Answer: (a) - Exterior angle at C = ?
(a) 110° (b) 120° (c) 130° (d) 140°
Answer: (a) - Exterior angle =
(a) sum of interior opposite (b) difference (c) product (d) none
Answer: (a) - If ∠A=50°, ∠B=60°, ∠C=?
Answer: 70°
Case Study 5: Clock Problem
At 3 o’clock, hands of a clock form an angle.
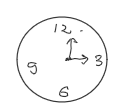
Questions:
- Angle between hour and minute hands =
(a) 60° (b) 90° (c) 75° (d) 120°
Answer: (b) - Hands of a clock are examples of:
(a) rays (b) lines (c) line segments (d) none
Answer: (a) - At 6 o’clock, angle formed =
(a) 180° (b) 90° (c) 120° (d) 60°
Answer: (a) - At 12 o’clock, angle formed =
(a) 0° (b) 180° (c) 90° (d) 60°
Answer: (a) - At 9 o’clock, angle formed =
(a) 180° (b) 90° (c) 120° (d) 60°
Answer: (b)
Case Study 6: Street Lamp
Two streets meet at right angles.
Questions:
- Angle formed =
(a) 45° (b) 90° (c) 120° (d) 180°
Answer: (b) - Right angle =
(a) 90° (b) 180° (c) 270° (d) 360°
Answer: (a) - Complement of 90° =
(a) 0° (b) 45° (c) 90° (d) none
Answer: (a) - Supplement of 90° =
(a) 45° (b) 90° (c) 180° (d) none
Answer: (c) - Right angle triangle has one angle =
(a) 45° (b) 90° (c) 60° (d) 30°
Answer: (b)
Case Study 7: Paper Fold
When a paper is folded diagonally, it creates intersecting lines at the center.
Questions:
- Opposite angles formed are:
(a) equal (b) unequal (c) complementary (d) none
Answer: (a) - Such angles are called:
(a) vertically opposite (b) linear pair (c) alternate (d) none
Answer: (a) - Angle sum around point =
(a) 90° (b) 180° (c) 270° (d) 360°
Answer: (d) - If one angle=120°, opposite angle=?
(a) 60° (b) 120° (c) 90° (d) none
Answer: (b) - Adjacent angles form:
(a) linear pair (b) equal pair (c) alternate (d) none
Answer: (a)
Case Study 8: Exterior Angle
In ΔABC, ∠A=40°, ∠B=60°. Find exterior angle at C.
Questions:
- ∠C=?
(a) 80° (b) 70° (c) 90° (d) 100°
Answer: (b) - Exterior angle at C=?
(a) 100° (b) 110° (c) 120° (d) 130°
Answer: (a) - Exterior angle property states:
(a) ext = sum of interior opposite (b) ext=diff (c) ext=product (d) none
Answer: (a) - Here, ∠A+∠B=?
(a) 100° (b) 110° (c) 120° (d) 130°
Answer: (a) - Exterior angle theorem is valid for:
(a) all triangles (b) only isosceles (c) only right angle (d) none
Answer: (a)
Case Study 9: Z-pattern Rule
Two parallel lines are cut by transversal, forming Z-shaped angles.
Questions:
- These angles are:
(a) corresponding (b) alternate interior (c) vertically opposite (d) none
Answer: (b) - If one angle=75°, alternate interior=?
(a) 105° (b) 75° (c) 90° (d) none
Answer: (b) - If transversal is ⟂, angle=?
(a) 90° (b) 120° (c) 180° (d) none
Answer: (a) - Rule is called:
(a) Z-rule (b) C-rule (c) F-rule (d) none
Answer: (a) - Alternate angles formed are:
(a) equal (b) unequal (c) supplementary (d) none
Answer: (a)
Case Study 10: Polygon Angles
In quadrilateral ABCD, ∠A=80°, ∠B=90°, ∠C=100°, find ∠D.
Questions:
- Sum of all angles in quadrilateral =
(a) 180° (b) 270° (c) 360° (d) none
Answer: (c) - ∠D=?
(a) 80° (b) 85° (c) 90° (d) 95°
Answer: (d) - Property used:
(a) Sum of interior angles of quadrilateral = 360° (b) exterior angle theorem (c) parallel lines (d) none
Answer: (a) - In polygon with n sides, sum of angles =
(a) (n−2)×180° (b) n×180° (c) (n+2)×180° (d) none
Answer: (a) - For triangle (n=3), sum=
(a) 120° (b) 180° (c) 360° (d) none
Answer: (b)
